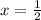Question

Find the maximum/minimum value of y = x2 - x + 1/4. At what value of x it occurs?

Answer 1

f(x) has a minimum value is zero at
`x = (1)/(2)`

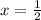
Explanation:

Explanation:-

step(i):-

Given function y =f(x)= x² - x + 1/4 ....(i)

Differentiating equation (i) with respective to 'x', we get

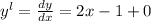`y^(l) =(d y)/(d x) = 2 x -1 +0` ...(ii)

Equating Zero 2 x - 1 = 0

`2 x = 1`

`x = (1)/(2)`

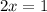
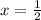
Step(ii):-

Again differentiating with respective to 'x', we get

`y^(ll) =(d^2 y)/(d x^2) = 2 (1) >0`

f(x) has a minimum value at
`x = (1)/(2)`

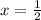
Step(iii):-

y =f(x) = x² - x + 1/4

Put
`x = (1)/(2)`

`f( (1)/(2)) = ((1)/(2) )2-(1)/(2) +(1)/(4)`

`f((1)/(2) ) = (2)/(4) -(1)/(2)`

`f((1)/(2) ) = 0`

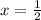
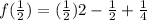
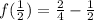
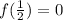
f(x) has a minimum value is zero at
`x = (1)/(2)`