Question

If f(x)=x^2 is vertically compressed by a factor of 8 yo g(x) , what is the equation of g(x)

Answer 1

`g(x)=(1)/(8) x^(2)`

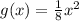
Explanation:

Expansions and compressions are transformations that change the length or width of the graph of a function. The general form of the graph of a function expands or compresses vertically or horizontally. Expansions and compressions are considered non-rigid transformations.

Vertical compression:

`y=kf(x)`

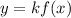
• If k>0 the graph of f (x) is vertically stretched by a factor of k.

• If k<0 the vertical stretch is followed by a reflection across the x-axis.

• If 0<k<1 the graph is f (x) vertically compressed by a factor of 1/k.

So, if
`f(x)=x^(2)` is vertically compressed by a factor of 8. Hence, using the previous information, we can conclude that the equation of
`g(x)` is:

`g(x)=(1)/(8) x^(2)`

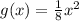
I attached you the graphs.