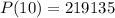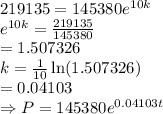Answer:
The exponential growth function is
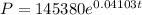
Explanation:
Given: The population of a certain city was 145,380 in 2000 and 219,135 in 2010.
To find: exponential growth function that models the growth of the city
Solution:
The exponential growth function is given by

Here, P denotes total population after time t
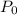 denotes initial population
denotes initial population
k denotes rate of growth
t denotes time
As
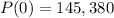 ,
,
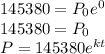
As