Question

Identify the 9th term of the given geometric sequence. [/tex]1/3, −1/9, 1/27, −1/81, ....

HELP ASAP PLEASE!!!

Answer 1

^^ what he said xD

Explanation:

It was snowing again and I smiled as I stared at the white flakes fluttering by my window. It was (capitalized the C)Christmas, and my day had been one of the best all year. First I (had removed) awakened in the morning to the sound of my brother (added the n to runing)running madly around the house, yelling that it was Christmas. Jumping out of bed, (capitalized the i that was there)I skipped happily down the stairs, with my brother at my heels, and made my way to the Christmas tree in the living room. My parents(apostrophe removed from between the t and s) groggily walked down the stairs to watch us open (up removed) our presents. My Mom sat down on the couch and dad plopped himself on the floor, grumbling something about coffee. I started opening my presents because, after all, its ladies first. Ripping open the wrapping paper, I stared down at my brand(removed dash)new pink boom box. It was beautiful!(question mark changed to exclamation) (capitalized e)Even more, it came with little, stick-on jewels to decorate the boom box. Mom and Dad finally got their coffee and we all took turns watching each other open presents. I got(get turned to got) many more presents that were absolutely amazing. (changed every one into one word)Everyone spends the rest of the day admiring their gifts and playing with their new toys. "I will remember this Christmas forever,"(added endnote) I thought. (capitalized s)Sighing contentedly, I finally turned away from the snow (removed the e from what was danceing)dancing outside the window and rejoined my family.

Answer 2

Explanation:

Before we find the ninth term, we need to find the common ratio. The common ratio in a geometric sequence is the number that every number after the first one is multiplied by. For example, in the sequence {2, 4, 8, 16, 32, ...}, the common ratio is 2.

Now, for our example, the numbers in the sequence alternate between negative and positive numbers. What does that tell us about the common ratio? Well, the common ratio has to be negative because the negative sign keeps alternating.

So we know the common ratio is negative. But what about the rest of the number? Well, we can see that the ratio has a 1 in the numerator because the numerator is the same throughout the sequence (aside from the alternating negative sign).

Now that we've narrowed down the possibilities to -1/x, let's figure out the denominator of the common ratio. The denominator changes from 3 to 9 to 27 to 81. Do you see a pattern there? Each denominator is 3 times the value of the previous denominator. The denominator of the common ratio, then, must be 3.

Ok. We have our common ratio, -1/3, but the question we still need to find the 9th term in the sequence. Well, we can write out the pattern until we get to the term we want. But what if you were trying to find the one hundredth or the one thousandth term? That would take a very long time to write out. Instead, we can take the first number in the sequence (1/3) and multiply it by the our common factor to the power of the remaining terms. As a formula, this looks like:
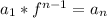`a_(1) *f^(n-1) = a_(n)`, where a is your first term, f is your common factor and n is the number of the term you are trying to find.

So, finally, we can solve the problem.

1/3 * (-1/3)⁸ = a₉

1/3 * 1/6561 = 1/19683

So the value of the ninth term of the given geometric sequence is 1/19683.

I hope you learned something and it wasn't too difficult to understand.