Question

Two ships leave at harbor at the same time. When ship travels on a bearing South 13° west at 15 mph. The other ship travels on a bearing north 75° east at 11 mph. How far apart with the ships be after two hours

Answer 1

44.76 miles

Explanation:

• Distance =Speed X Time

The First Ship travels at 15 mph from A to C

Distance covered in 2 hours =15 X 2 =30 Miles

The Second Ship travels at 11 mph from A to B

Distance covered in 2 hours =11 X 2 =22 Miles

The path of the two ships forms a triangle ABC where:

AB=22 Miles

AC=30 miles

`\angle A=13^\circ+90^\circ+15^\circ\\\angle A=118^\circ`

We want to determine the distance BC between the two ships.

Using Law of Cosines

`a^2=b^2+c^2-2bc\cos A\\a^2=30^2+22^2-2*30*22\cos 118^\circ\\a^2=2003.7025\\a=√(2003.7025)\\a=44.76$ miles`

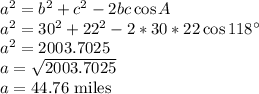
BC= 44.76 miles

After two hours, the two ships are 44.76 miles apart.