Question

Weights of Minivans The average weight of 40 ran- domly selected minivans was 4150 pounds. The popula- tion standard deviation was 480 pounds. Find a point es- timate of the population mean. Find the 99% confidence interval of the true mean weight of the minivans.

Answer 1

99% confidence interval of the true mean weight of the minivans

(3954.192 ,4345.808)

Explanation:

step(i):-

Given sample size 'n' = 40

mean of the sample x⁻ = 4150 pounds

Standard deviation of the Population 'σ' = 480 pounds

Critical value:-

`Z_{(\alpha )/(2) } = Z_{(0.01)/(2) } = Z_(0.005) = 2.58`

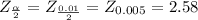
step(ii):-

99% confidence interval of the true mean weight of the minivans

`(x^(-) - Z_{(\alpha )/(2) } (S.D)/(√(n) ) , x^(-) - Z_{(\alpha )/(2) } (S.D)/(√(n) ))`

`(4150 - 2.58 (480)/(√(40) ) , 4150 - 2.58 (480)/(√(40) ))`

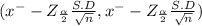
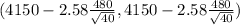
(4150 - 195.808 , 4150 + 195.808)

(3954.192 ,4345.808)

Conclusion:-

99% confidence interval of the true mean weight of the minivans

(3954.192 ,4345.808)