Answer:
a)
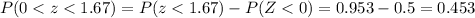
b)

c)
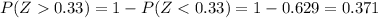
d)
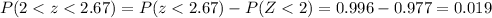
Explanation:
Assuming the following questions:
a. Between 20 and 25 gallons
Let X the random variable that represent the sports drink consumption of a population, and for this case we know the distribution for X is given by:
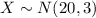
Where
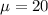 and
and
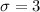
We are interested on this probability
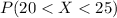
And the best way to solve this problem is using the normal standard distribution and the z score given by:

And if we find the z score for each limit we got:

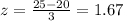
And we can use the normal standard distirbution table and we got:
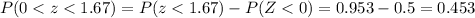
b. Less than 19 gallons
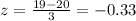
And using the normal table we got:

c. More than 21 gallons
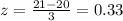
And using the normal table and the complement rule we got:
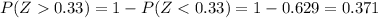
d. Between 26 and 28 gallons

![z = (28-20)/(3)=2.67/tex]</p><p>And we can use the normal standard distirbution table and we got:</p><p>[tex] P(2<z<2.67)= P(z<2.67) -P(Z<2) = 0.996 -0.977=0.019]()