Question

Walter invests $100,000 in an account that compounds interest continuously and earns 12%. How long will it take for his money to triple? Round to the nearest tenth of a year.

Answer 1

`300000= 100000 e^(0.12 t)`

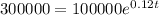
We divide both sides by 100000 and we got:

`3 = e^(0.12 t)`

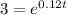
Now we can apply natural logs on both sides;

`ln(3) = 0.12 t`

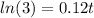
And then the value of t would be:

`t = (ln(3))/(0.12)= 9.16 years`

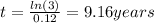
And rounded to the nearest tenth would be 9.2 years.

Explanation:

For this case since we know that the interest is compounded continuously, then we can use the following formula:

`A =P e^(rt)`

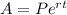
Where A is the future value, P the present value , r the rate of interest in fraction and t the number of years.

For this case we know that P = 100000 and r =0.12 we want to triplicate this amount and that means
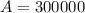`A= 300000` and we want to find the value for t.

`300000= 100000 e^(0.12 t)`

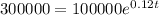
We divide both sides by 100000 and we got:

`3 = e^(0.12 t)`

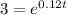
Now we can apply natural logs on both sides;

`ln(3) = 0.12 t`

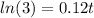
And then the value of t would be:

`t = (ln(3))/(0.12)= 9.16 years`

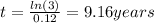
And rounded to the nearest tenth would be 9.2 years.