Question

A puck company wants to sponsor the players with the 10% quickest goals in hockey games. The times of first goals are normally distributed with a mean of 8.54 minutes and a standard deviation of 4.91 minutes. How fast would a player need to make a goal to be sponsored by the puck company?

Answer 1

`z=-1.28<(a-8.54)/(4.91)`

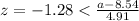
And if we solve for a we got

`a=8.54 -1.28*4.91=2.2552`

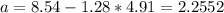
And for this case we can conclude that the time required needs to be 2.2552 minutes or less in order to be sponsored

Explanation:

Let X the random variable that represent the time for goals in hockey games of a population, and for this case we know the distribution for X is given by:

`X \sim N(8.54,4.91)`

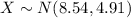
Where
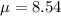`\mu=8.54` and
`\sigma=4.91`

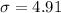
For this part we want to find a value a, such that we satisfy this condition:

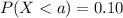`P(X<a)=0.10` (a)

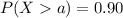`P(X>a)=0.90` (b)

As we can see on the figure attached the z value that satisfy the condition with 0.10 of the area on the left and 0.90 of the area on the right it's z=-1.28.

If we use condition (b) from previous we have this:

`P(X<a)=P((X-\mu)/(\sigma)<(a-\mu)/(\sigma))=0.10`

`P(z<(a-\mu)/(\sigma))=0.10`

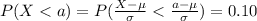
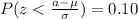
and we can do the following

`z=-1.28<(a-8.54)/(4.91)`

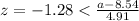
And if we solve for a we got

`a=8.54 -1.28*4.91=2.2552`

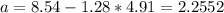
And for this case we can conclude that the time required needs to be 2.2552 minutes or less in order to be sponsored