Answer:
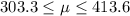
We need to remember that the confidence interval for the true mean is given by:
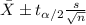
Since the upper limit for the confidence interval is lower than the value of 425 we don't have enough evidence to conclude that the the mean skidding distance is at least 425 meters at the 5% of signficance used so then the confidence interval not support the loggers claim
Explanation:
We know that they use a sample size of n =20 and the confidence interval for the true mean skidding distance along a new road in a European forest is given by:
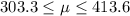
We need to remember that the confidence interval for the true mean is given by:
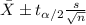
Since the upper limit for the confidence interval is lower than the value of 425 we don't have enough evidence to conclude that the the mean skidding distance is at least 425 meters at the 5% of signficance used so then the confidence interval not support the loggers claim