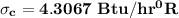Answer:
a)
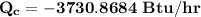
b)
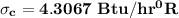
Step-by-step explanation:
From the properties of Super-heated Refrigerant 134a Vapor at
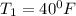 ,
,
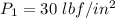 ; we obtain the following properties for specific enthalpy and specific entropy.
; we obtain the following properties for specific enthalpy and specific entropy.
So; specific enthalpy
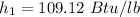
specific entropy
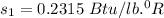
Also; from the properties of saturated Refrigerant 134 a vapor (liquid - vapor). pressure table at
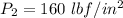 ; we obtain the following properties:
; we obtain the following properties:

Given that the power input to the compressor is 2 hp;
Then converting to Btu/hr ;we known that since 1 hp = 2544.4342 Btu/hr
2 hp = 2 × 2544.4342 Btu/hr
2 hp = 5088.8684 Btu/hr
The steady state energy for a compressor can be expressed by the formula:

By neglecting kinetic and potential energy effects; we have:
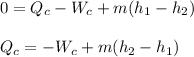
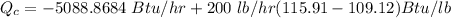
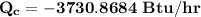
b) To determine the entropy generation; we employ the formula:
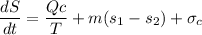
In a steady state condition

Hence;

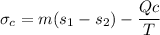
![\sigma _c = [200 \ lb/hr (0.2157 -0.2315) \ Btu/lb .^0R - ((-3730.8684 \ Btu/hr))/((40^0 + 459.67^0)^0R)]](https://img.qammunity.org/2021/formulas/engineering/college/9fg98amkedgk6nsq7h6ru4cu0f2xsmufh5.png)
![\sigma _c = [(-3.16 ) \ Btu/hr .^0R + (7.4667 ) Btu/hr ^0R}]](https://img.qammunity.org/2021/formulas/engineering/college/jdy7oyrjvc590uqu15mtzislqavof5xmyp.png)