Question

You manage a risky portfolio with an expected rate of return of 18% and a standard deviation of 30%. The T-bill rate is 6%. Your client chooses to invest 65% of a portfolio in your fund and 35% in an essentially risk-free money market fund. What is the expected return and standard deviation of the rate of return on his portfolio?

Answer 1

Step-by-step explanation:

Expected return of the portfolio is weighted average of the return of the components.

E(R) = w1 * R1 + w2 * R2

E(R) = 65% * 18% + 35% * 6%

E(R) = 11.70% + 2.10%

Expected Return, E(R) = 13.80%

Standard deviation of portfolio is mathematically represented as:

`\sigma =\sqrt{w_1^2\sigma _1^2+w_2^2\sigma _2^2+2w_1w_2p_(1,2)\sigma_1\sigma_2}`

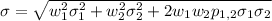
where

w1 = the proportion of the portfolio invested in Asset 1

w2 = the proportion of the portfolio invested in Asset 2

σ1 = Asset 1 standard deviation of return

σ2 = Asset 2 standard deviation of return

For risk free money market fund, standard deviation = 0 and its correlation with risky portfolio = 0

`\sigma =√( (0.65 * 0.30)^2 + (0.35 * 0)^2 + (2 * 0.65 * 0.30*0.35 *0*0)) \\\\= √(0.038025 +0+0) \\\\ = 0.195`

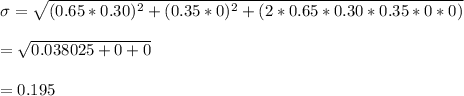
Standard deviation = 19.50%