Question

What is the approximate length of a pendulum that takes 2.4 pi seconds to swing back and forth?

1.72 ft

3.05 ft

38.40 ft

46.08 ft

Answer 1

46.08 ft

Explanation:

Answer 2

The approximate length of the pendulum is 46.08 ft

Explanation:

The time (t) of pendulum oscillation is given as;

`t = 2 \pi\sqrt{(L)/(g) }`

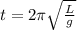
where;

L is the length of the pendulum

g is acceleration due to gravity = 9.8 m/s² = 32.15 ft/s²

t is the time given as 2.4 π seconds

From the equation above, make L the subject of the formula;

`t = 2 \pi\sqrt{(L)/(g) } \\\\(t)/(2\pi) = \sqrt{(L)/(g) }\\\\((t)/(2\pi) )^2 =(L)/(g) \\\\L = g*((t)/(2\pi) )^2\\\\L = 32.15*((2.4 \pi)/(2\pi) )^2\\\\L = 32.15 *1.44\\\\L = 46.296 \ ft`

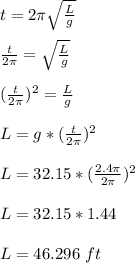
Therefore, the approximate length of the pendulum is 46.29 ft

The closest option is 46.08 ft