Answer: 34) 15 35) 4, 4, 3 36) 1, 4
Explanation:
34)
Let Triangle = T, Circle = C, and Square = S, and Pentagon = P
Top Row: 4T = 8 --> T = 2
2nd column: 2T + 2C = 10 --> C = 3
2nd row: S + T + 2C = 12 --> S = 4
1st column: T + 2S + P = 15 --> P = 5
3rd column: x = T + C + 2P
= 2 + 3 + 2(5)
= 15
35)
Fill in the puzzle as follows:
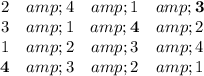
A = 4, B = 4, C = 3
36)
Notes:
U = x
means that everything within the rectangular box (including the circles) contains the Natural Numbers of 3 through 14, including 3 but excluding 14.
R = 5 ≤ x ≤ 8, x ∈ N
means that everything within the circle of R (including the intersection with T) contains the Natural Numbers of 5 through 8, including 5 and 8.
T = {4, 7, 10, 13}
means that everything within the circle of T (including the intersection with R) contains 4, 7, 10, & 13.
Filling in the Venn Diagram (from left to right):
R (only) contains 5, 6, 8
R ∩ T (the middle section of R and T) contains 7
T (only) contains 4, 10, 13
outside the circles but inside the rectangle (usually written on the lower left corner) is 3, 9, 11, 12
Statements:
1) R ∩ T = {7}
means the intersection of R and T (the middle circle) contains 7 and nothing else.
Refer to your Venn Diagram. This statement is TRUE!
2) n(R ∪ T)' = 6
means the QUANTITY of numbers NOT in both R & T is 6.
The numbers that are not in either R or T are: 3, 9, 11, 12.
That results in 4 numbers (not 6). This statement is False.
3) n(R' ∩ T) = 2
means the QUANTITY of numbers that are NOT in R but are in T is 2.
The numbers that are not in R but are in T are: 4, 10, 13.
That results in 3 numbers (not 2). This statement is False.
4) n(R ∩ T') = 3
means the QUANTITY of numbers that are in R but NOT in T is 3.
The numbers that are in R but NOT in T are: 5, 6, 8.
That results in 3 numbers. This statement is True!