Question

If p=(-3,-2) and q=(1,6) are the endpoints of the diameter of a circle find the equation of the circle

Answer 1

-1 , 2 , 20

Explanation:

( x - -1 ) ² + ( y - 2 ) ² = 20

Answer 2

The equation of the circle (x +1) )² +(y-(2))² = (2(√5))²

or

The equation of the circle x² + 2 x + y² - 4 y = 15

Explanation:

Given points end Points are p(-3,-2) and q( 1,6)

The distance of two points formula

P Q =
`\sqrt{x_(2) - x_(1))^(2) + ((y_(2) -y_(1))^(2) }`

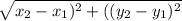
P Q =
`\sqrt{1 - (-3)^(2) + ((6 -(-2))^(2) }`

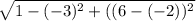
P Q =
`√(16+64) = √(80)`

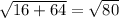
The diameter 'd' = 2 r

2 r = √80

=
`√(16 X 5)`

=
`4 √(5)`

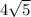
r = 2√5

Mid-point of two end points

`((x_(1) + x_(2) )/(2) , (y_(1) +y_(2) )/(2) ) = ((-3+1)/(2) ,(-2 +6)/(2) )`

= (-1 ,2)

Mid-point of two end points = center of the circle

(h,k) = (-1 , 2)

The equation of the circle

(x -h )² +(y-k)² = r²

(x -(-1) )² +(y-(2))² = (2(√5))²

x² + 2 x + 1 + y² - 4 y + 4 = 20

x² + 2 x + y² - 4 y = 20 -5

x² + 2 x + y² - 4 y = 15

Final answer:-

The equation of the circle (x +1) )² +(y-(2))² = (2(√5))²

or

The equation of the circle x² + 2 x + y² - 4 y = 15