Question

Prove that the median to the hypotenuse of a right triangle is half the hypotenuse. Proof: By the Distance Formula, MN = _. Therefore, OP=1/2 MN.

Answer 1

Option (A).

Explanation:

From the figure attached,

ΔMON is a right triangle and coordinates of the points M and N are M(0, 2b) and N(2a, 0).

Coordinates of midpoint P →
`((2a+0)/(2), (0+2b)/(2))`

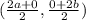
→ (a, b)

From the formula of the distance between two points,

d =
`\sqrt{(x_(2)-x_(1))^2+(y_(2)-y_(1))^2}`

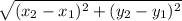
MN =
`√((2a-0)^2+(0-2b)^2)`

=
`√(4a^2+4b^2)`

= 2
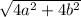
`√(a^2+b^2)`

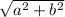
Similarly, OP =
`√((0-a)^2+(0-b)^2)`

=
`√(a^2+b^2)`

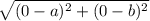
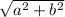
Therefore, OP =
`(1)/(2)(MN)`

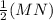
and MN =
`√(4a^2+4b^2)` = 2
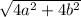`√(a^2+b^2)`

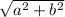
Option (a) is the answer.