Question

9. Sarah buys a car for $11,385. She has no car to

trade in. Her down payment is $1385. If she
takes out a loan at 13% interest for 5 years,
how much will the monthly payments be?
Answer

Answer 1

`\fbox{\begin{minipage}{13em}approximately 318.143 dollars\end{minipage}}`

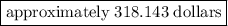
Explanation:

Given:

Sarah buys a car for $11,385.

Her down payment is 1385$.

A loan is taken out for completing this contract, at 13% interest rate for 5 years.

Solve for:

Monthly payments.

Solutions:

Step 1: Apply the correct formula

a, To workout the actual amount of money (AM) that must be paid back to bank, the following formula is used:

AM = Principal x (1 + rate)^time

b, This amount of money is then divided by number of months in 5 years to get the monthly payment.

Step 2: Perform the calculation

After the down payment step, the loan Sarah took out to pay off the price of that car: L = 11385 - 1385 = 10000

The total amount of money she will need to pay back bank after 5 years, with principal = L, interest rate = 13%:

AM = 10000 x (1 + (13/100)/12)^(5 x 12) = 19088.565$

=> The monthly payment is:

MP = total amount of money/number of months

= 19088.565/(5 x 12) = ~318.143$

Hope this helps!

:)