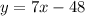Question

Complete the equation of the line through (6,-6 ) and (8, 8) Use exact numbers. y=

Answer 1

`m =(y_2 -y_1)/(x_2 -x_1)`

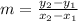
And replacing we got:

`m=(8-(-6))/(8-6)= 7`

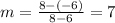
And now we can use one of the points and we can find the intercept b like this:

`8 = 7*8 +b`

And solving for b we got:

`b = 8 -56 = -48`

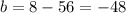
And the line would be:

`y = 7x -48`

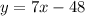
Explanation:

For this case we have two points given :

(x1=6,y1=-6) and (x2=8,y2=8)

We can find the line equation given by:

`y = mx+b`

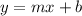
The slope would be:

`m =(y_2 -y_1)/(x_2 -x_1)`

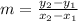
And replacing we got:

`m=(8-(-6))/(8-6)= 7`

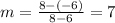
And now we can use one of the points and we can find the intercept b like this:

`8 = 7*8 +b`

And solving for b we got:

`b = 8 -56 = -48`

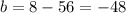
And the line would be:

`y = 7x -48`