Question

According to the Mortgage Bankers Association, 21% of U.S. mortgages were delinquent last year. A delinquent mortgage is one that has missed at least one payment but has not yet gone to foreclosure. A random sample of seven mortgages was selected. What is the standard deviation of this distribution

Answer 1

The standard deviation for the number of delinquent mortgages in the sample is 1.08.

Explanation:

For each mortgage, there are only two possible outcomes. Either it is delinquent, or it is not. The probability of a mortgage being delinquent is independent of other mortgages. So we use the binomial probability distribution to solve this question.

Binomial probability distribution

Probability of exactly x sucesses on n repeated trials, with p probability.

The standard deviation of the binomial distribution is:

`√(V(X)) = √(np(1-p))`

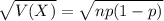
21% of U.S. mortgages were delinquent last year.

This means that
`p = 0.21`

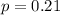
A random sample of seven mortgages was selected.

This means that
`n = 7`

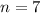
What is the standard deviation of this distribution

`√(V(X)) = √(7*0.21*0.79) = 1.08`

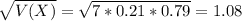
The standard deviation for the number of delinquent mortgages in the sample is 1.08.