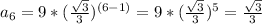Question

Determine the common ratio and find the next three terms of the geometric sequence 9,3sqrt3,3

Answer 1

Fourth term:
`a_4 = 9 * ((√(3))/(3))^((4 - 1))` =
`9 * ((√(3))/(3))^(3)` =
`√(3)`

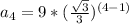Fifth term:
`a_5 = 9 * ((√(3))/(3))^((5 - 1))` =
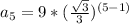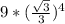`9 * ((√(3))/(3))^(4)` = 1

Sixth term:
`a_6 = 9 * ((√(3))/(3))^((6 - 1)) = 9 * ((√(3))/(3))^(5) =(√(3))/(3)`

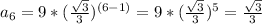
Explanation:

The geometric progression is:

`9, 3 √(3), 3...`

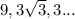
The first term, a, is 9

To find the common ratio, r, all we have to do is divide a term by its preceding term.

Let us divide the second term by the first:

`r = (3√(3))/(9)\\ \\r = (√(3))/(3)`

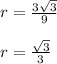
That is the common ratio.

Geometric progression is given generally as:

`a_n = ar^((n - 1))`

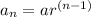
where a = first term

r = common ratio

`a_n` = nth term

We need to find the 4th, 5th and 6th terms.

Fourth term:
`a_4 = 9 * ((√(3))/(3))^((4 - 1))` =
`9 * ((√(3))/(3))^(3)` =
`√(3)`

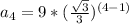Fifth term:
`a_5 = 9 * ((√(3))/(3))^((5 - 1))` =
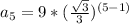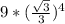`9 * ((√(3))/(3))^(4)` = 1

Sixth term:
`a_6 = 9 * ((√(3))/(3))^((6 - 1)) = 9 * ((√(3))/(3))^(5) =(√(3))/(3)`