Question

Determine the quadrant in which the terminal side of the given angle lies.

115°

A. I

B. II

C. III

D. IV

Answer 1

`(x)/(115)= (2\pi)/(360)`

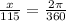
And solving for x we got:

`x= (115)/(160) 2\pi = (23)/(36)pi= 0.639 \pi`

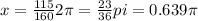
since the value obtained is higher than
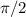`\pi/2` and lower than
`\pi` we can conclude that this angle would be in the second quadrant.

B. II

Explanation:

In order to solve this problem we can write the angle in terms of pi using the following proportion rule:

`(x)/(115)= (2\pi)/(360)`

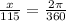
And solving for x we got:

`x= (115)/(160) 2\pi = (23)/(36)pi= 0.639 \pi`

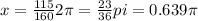
since the value obtained is higher than
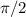`\pi/2` and lower than
`\pi` we can conclude that this angle would be in the second quadrant.

B. II