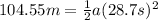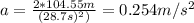Question

A man starts with an initial velocity of 3.50 m/s and accelerates for a distance of 205

m over 28.7 s. What is the acceleration of the man?

Answer 1

`X= v_i t + (1)/(2)a t^2`

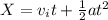
And from this equation we can solve for a like this:

`205m = 3.5m/s *(28.7s) +(1)/(2)a (28.7s)^2`

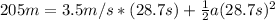
And solving for a we got:

`104.55m = (1)/(2)a (28.7s)^2`

`a = (2*104.55m)/((28.7s)^2))= 0.254 m/s^2`

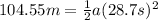
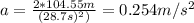
Explanation:

For this case we have the velocity , distance and time given:

`v = 3.5 m/s, d=205m, t =28.7s`

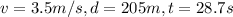
And we know from kinematics that he velocity can be expressed like this:

`v_f = v_i +a t`

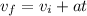
We also know that the distance is given by:

`X= v_i t + (1)/(2)a t^2`

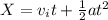
And from this equation we can solve for a like this:

`205m = 3.5m/s *(28.7s) +(1)/(2)a (28.7s)^2`

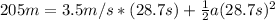
And solving for a we got:

`104.55m = (1)/(2)a (28.7s)^2`

`a = (2*104.55m)/((28.7s)^2))= 0.254 m/s^2`