Answer:
Explanation:
(a) If the state space is taken as
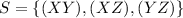 , the probability of transitioning from one state, say (XY) to another state, say (XZ) will be the same as the probability of Y losing out to X, because if X and Y were playing and Y loses to X, then X and Z will play in the next match. This probability is constant with time, as mentioned in the question. Hence, the probabilities of moving from one state to another are constant over time. Hence, the Markov chain is time-homogeneous.
, the probability of transitioning from one state, say (XY) to another state, say (XZ) will be the same as the probability of Y losing out to X, because if X and Y were playing and Y loses to X, then X and Z will play in the next match. This probability is constant with time, as mentioned in the question. Hence, the probabilities of moving from one state to another are constant over time. Hence, the Markov chain is time-homogeneous.
(b) The state transition matrix will be:
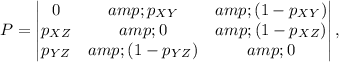
where as stated in part (b) above, the rows of the matrix state the probability of transitioning from one of the states
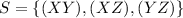 (in that order) at time n and the columns of the matrix state the probability of transitioning to one of the states
(in that order) at time n and the columns of the matrix state the probability of transitioning to one of the states
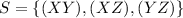 (in the same order) at time n+1.
(in the same order) at time n+1.
Consider the entries in the matrix. For example, if players X and Y are playing at time n (row 1), then X beats Y with probability
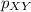 , then since Y is the loser, he sits out and X plays with Z (column 2) at the next time step. Hence, P(1, 2) =
, then since Y is the loser, he sits out and X plays with Z (column 2) at the next time step. Hence, P(1, 2) =
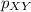 . P(1, 1) = 0 because if X and Y are playing, one of them will be a loser and thus X and Y both together will not play at the next time step.
. P(1, 1) = 0 because if X and Y are playing, one of them will be a loser and thus X and Y both together will not play at the next time step.
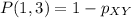 , because if X and Y are playing, and Y beats X, the probability of which is
, because if X and Y are playing, and Y beats X, the probability of which is
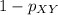 , then Y and Z play each other at the next time step. Similarly,
, then Y and Z play each other at the next time step. Similarly,
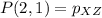 , because if X and Z are playing and X beats Z with probability
, because if X and Z are playing and X beats Z with probability
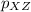 , then X plays Y at the next time step.
, then X plays Y at the next time step.
(c) At equilibrium,
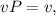
i.e., the steady state distribution v of the Markov Chain is such that after applying the transition probabilities (i.e., multiplying by the matrix P), we get back the same steady state distribution v. The Eigenvalues of the matrix P are found below:
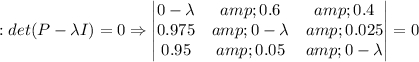
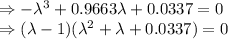
The solutions are
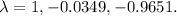 These are the eigenvalues of P.
These are the eigenvalues of P.
The sum of all the rows of the matrix
 is equal to 0 when
is equal to 0 when
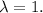 Hence, one of the eigenvectors is :
Hence, one of the eigenvectors is :
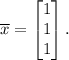
The other eigenvectors can be found using Gaussian elimination:
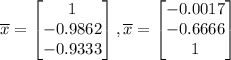
Hence, we can write:
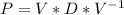 , where
, where

and
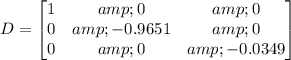
After n time steps, the distribution of states is:
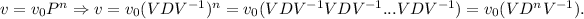
Let n be very large, say n = 1000 (steady state) and let v0 = [0.333 0.333 0.333] be the initial state. then,
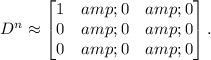
Hence,
![v=v_0(VD^nV^(-1))=v_0(V\begin{bmatrix} 1 & 0 & 0\\ 0 &0 &0 \\ 0& 0 & 0 \end{bmatrix}V^(-1))=[0.491, 0.305, 0.204].](https://img.qammunity.org/2021/formulas/mathematics/college/jmuiiyas9ovxxo9e8ka53njqzo482cx1ec.png)
Now, it can be verified that
![vP = [0.491, 0.305,0.204]P=[0.491, 0.305,0.204].](https://img.qammunity.org/2021/formulas/mathematics/college/eithbkozo55zxmr3ven9x0zghzt25j5b6a.png)