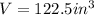Answer:
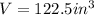
Explanation:
The volume of a right circular cone is given by:
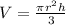
where r is the radius of the circle and h is the height of the cone, and
 is a constant
is a constant
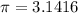 .
.
According to the problem the height is:
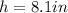
and we don't have the radius but we have the diameter, which is useful to find it. We just divide the diameter by 2 to find the radius:
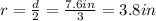
Now, we can find the volume by substituting all the known values:
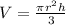

Rounding the volume to the nearest tenth of cubic inch we get: