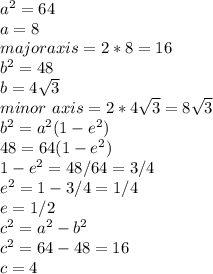Answer:
Explanation:
r=24/(4+2sin θ)
4r+2r sin θ=24
divide by 2
2r+r sin θ=12
2√(x²+y²)+y=12
2√(x²+y²)=12-y
squaring
4(x²+y²)=144-24y+y²
4x²+3y²+24y=144
4x²+3(y²+8y+16-16)=144
4x²+3(y+4)²-48=144
4x²+3(y+4)²=144+48
4x²+3(y+4)²=192
divide by 192
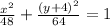
which is an ellipse with centre(0,-4) major axis on y-axis.