Answer:
Option D. 82.8°
Explanation:
From the figure attached,
By using Cosine rule in the given triangle ABC,
AC² = AB² + BC ² - 2(AB)(BC)cosB
(12)² = (8)² + (10)² - 2(8)(10)cosB
144 = 64 + 100 - 160.(cosB)
144 = 164 - 160.(cosB)
160.(cosB) = 164 - 144
cosB =
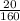
cosB =
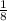
B =
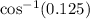
B = 82.82°
B ≈ 82.8°
Therefore, Option D. will be the answer.