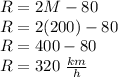Answer:
Malcolm's maximum speed is
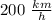
Ravi's maximum speed is
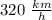
Explanation:
Notice that this is a problem with two unknowns: the max speed of Malcolm (let's name this "M"), and the max speed of Ravi (let's name this R). So we need to build two equations with them, based on the information given.
Equation 1: based on the phrase "The average of their maximum speeds was 260 km/h" we write the equation for average (addition of both speeds, divided by 2, equal 260 km/h:
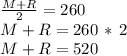
Equation 2; based on the phrase: "If doubled, Malcolm's max speed would be 80 km/h more than Ravi's max speed"

We can now use for example substitution to solve the system of equations
From the second equation we created, we can solve for R in terms on M:
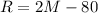
and use it as substitution in the first equation:

And now use this value of M in the substitution equation to solve for R;