Question

Help. I can't do maths again​

Answer 1

x ≈ 14.4 cm

Explanation:

the third angle of the triangle = 180° - 40° - 46° = 94°

Using the Sine rule in the triangle

`(x)/(sin46)` =
`(20)/(sin94)` ( cross- multiply )

x × sin94° = 20 × sin46° ( divide both sides by sin94° )

x =
`(20sin46)/(sin94)` ≈ 14.4 cm ( to the nearest tenth )

Answer 2

14 cm (rounded to nearest whole number)

Explanation:

Law of Sine:

`\displaystyle \large{(\sin A)/(a) = (\sin B)/(b) = (\sin C)/(c) = 2R}`

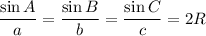
• a,b,c are side lengths.
• R is radius so 2R is diameter.
• A,B,C are angles.

Given angles are:

• 40°, 46°

Definition of Euclidean Triangle:

• Sum of three interior angles equals 180°

Find another angle:

• 40°+46°+B = 180°
• 86+B = 180
• B = 180-86
• B = 94°

So another angle is 94°.

To find:

• Value of x

Determine:

• A = 46°
• a = x cm
• B = 94°
• b = 20 cm

Therefore:

`\displaystyle \large{(\sin 46^(\circ))/(x) = (\sin 94^(\circ))/(20)}`

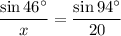
Multiply both sides by 20x:

`\displaystyle \large{(\sin 46^(\circ))/(x) \cdot 20x = (\sin 94^(\circ))/(20) \cdot 20x}\\\displaystyle \large{20\sin 46^(\circ)= x\sin 94^(\circ)}`

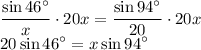
Divide both sides by
`\displaystyle \large{\sin 94^(\circ)}`:

`\displaystyle \large{(20\sin 46^(\circ))/(\sin 94^(\circ)) = (x\sin 94^(\circ))/(\sin 94^(\circ))}\\\displaystyle \large{(20\sin 46^(\circ))/(\sin 94^(\circ)) = x}`

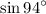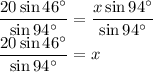
Evaluate the expression, hence:

`\displaystyle \large{x = 14.42...}`

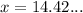
Round to nearest whole number:

`\displaystyle \large{x = 14}`

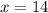
Therefore, the value of x is 14 cm.