Question

Suppose you are a chemist who is trying to synthesize a specific compound. You have been working with a new technique and you think that this process can turn 60% of the input compounds into the desired synthesized compound, and want to attempt the process enough times to get an estimate that is within .04 of the true proportion that is converted. How many times should you execute the process to get the desired precision

Answer 1

The sample size 'n' = 576

576 times should you execute the process to get the desired precision

Explanation:

Explanation :-

Step(i)

Given data the process can turn 60% of the input compounds into the desired synthesized compound.

Sample proportion ' p' = 60% = 0.60

Given data the estimate within 0.04 of the true proportion that is converted

The margin of error of the true population proportion

M.E = 0.04

Step(ii)

The margin of error of the true population proportion is determined by

`M.E = ( Z_(0.05) √(p(1-p)) )/(√(n) )`

`0.04 = ( 1.96 √(0.60(1-0.60)) )/(√(n) )`

`√(n) = ( 1.96 √(0.60(1-0.60)) )/(0.04 )`

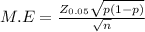
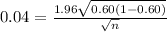
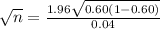
on calculation, we get

`√(n) = 24`

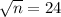
squaring on both sides ,we get

n = 576

Final answer:-

The sample size 'n' = 576

576 times should you execute the process to get the desired precision