Answer:
(A)(StartFraction d minus b Over c minus a EndFraction) (StartFraction c minus a Over negative d + b EndFraction) = negative 1
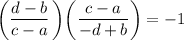
Explanation:
Given: Line PQ is rotated 90° counterclockwise to form line P’Q’. The lines are perpendicular. Line PQ contains the points (a, b) and (c, d). Line P’Q’ contains the points (–b, a) and (–d, c).
Prove: The slopes of perpendicular lines are negative reciprocals.
On a coordinate plane, 2 perpendicular lines are shown. Line P Q has points (a, b) and (c, d).
Line P prime Q prime has points (-b, a) and (-d, c).
The slopes of lines PQ and P’Q’ can be determined using the formula
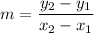
The product of these slopes is:
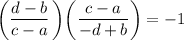
This product shows that the slopes are negative reciprocals. It is given that the lines are perpendicular and we have shown that the slopes of the lines are negative reciprocals.
The correct option is A.