Question

Find the radius round your answer to the nearest tenth

Answer 1

r = 3m

Explanation:

Formula for the volume of a sphere: V =
`(4)/(3)`
`\pi`
`r^(3)`

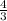
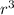
We want to find the radius so we use algebra to rearrange the equation to make the radius (r) the subject of the equation

Divide both sides by
`(4)/(3)`

`(3V)/(4)` =
`\pi`
`r^(3)`

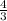
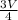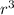
Divide both sides by
`\pi`

`(3V)/(4\pi )` =
`r^(3)`

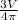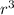
Take the cube root of both sides

`\sqrt[3]{(3V)/(4\pi ) }`= r

Substitute V = 36
`\pi` into the equation

r =
`\sqrt[3]{(3(36\pi) )/(4\pi ) }`

Expand the bracket

r =
`\sqrt[3]{(108\pi )/(4\pi ) }`

Divide 108
`\pi` by 4
`\pi` (For this, the two
`\pi` in the numerator and denominator cancel each other out, and you only need to divide 108/4)

r =
`\sqrt[3]{27}`

The cube root of 27 is 3, because
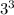`3^(3)` = 3 x 3 x 3 = 27

r = 3