Question

How to calculate Density of tetragonal unit cell by formula?

Answer 1

`\huge\underline{\red{A}\blue{n}\pink{s}\purple{w}\orange{e}\green{r} -}`

The formula of Density for a random unit cell is as follows -

`Density = \frac{ Z _(effective) * M }{N _(a) * a {}^(3) } \\`

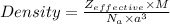
where ,

★
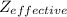`Z _(effective)` = number of atoms in a unit cell

★ M = molar mass

★
`N _(a) = Avogadro's \: Number = 6 × 10^(23)`

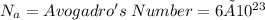
★ a = edge length

now ,

In a tetragonal unit cell ,

the atoms are present over the corners as well as the at the body centre.

Therefore ,

`Z _(effective) = contribution \: by \: the \: 8 \: corners \: + contribution \: by \: the \: body \: centre`

`\implies \: ((1)/(8) * 8) \: + \: 1 \\ \\ \implies \: 1 + 1 \\ \\ \implies2`

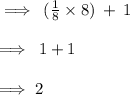
And ,

`N _(a) = 6 * 10 {}^(23)`

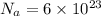
Substituting the values of the following in the formula of Density , we get

`\bold\purple{Density = \frac{2 * M}{6 * 10 {}^(23) * a {}^(3) }} \\`

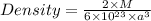
hope helpful :D