Question

The three sides of a triangle are (x+5)cm ,(2x+4)cm and (2x-3)cm .

a.find the perimeter of the triangle
b. if x =10, find the perimeter of the traingle.
​

Answer 1

Given ↓

• The three sides of the triangle : (x+5), (2x+4) and (2x-3)

To Find ↓

• The perimeter of the triangle

Calculations ↓

To find the perimeter of a shape, we should add all sides , like so :

x+5+2x+4+2x-3

Combine the x's :

x+2x+2x+5+4-3

x+4x+9-3

5x+6

Perimeter :

5x+6 cm

º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º

b.

Find the perimeter of the triangle if x = 10

Just write 10 instead of x :

5(10)+6

5(10) simplifies to 50 ↓

50+6

56

Perimeter of the triangle when x = 10 : 56 cm

hope helpful ~

Answer 2

Hey ! there

Answer:

• a. Perimeter = ( 5x + 6 ) cm

• b. Perimeter when x is equal to 10 = 56 cm

Explanation:

In this question we are given with three sides of a triangle that are as follows ,

• ( x + 5 ) cm

• ( 2x + 4 ) cm

• ( 2x - 3 ) cm

And we are asked to :

• a. find perimeter of triangle.

• b. find perimeter if x is equal to 10 .

We know that for finding perimeter of any shape we must have to add all the sides of the shape or ,

`\qquad \: \underline{\boxed{\frak{Perimeter = Sum \: of \: all \: sides}}}`

Solution : -

( a )

Now adding all the three sides of triangle to find the perimeter .

`\hookrightarrow \quad \: ( x + 5 ) + ( 2 x + 4 ) + ( 2x - 3 )`

`\hookrightarrow \quad \: \: x + 5 + 2x + 4 + 2x - 3`

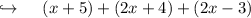
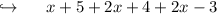
Combining like terms :

`\hookrightarrow \quad \:x + 2x + 2x + 5 + 4 - 3`

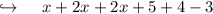
Now , solving :

`\hookrightarrow \quad \: \red{\underline{ \boxed{ \frak{(5x + 6) \: cm}}}}`

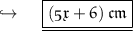
• Therefore , perimeter of triangle is 5x + 6 centimetres .

( b )

Now , we are finding perimeter of triangle when value of x is 10 . So substituting value of x in given sides of triangle ,

First Side :

• x + 5

• 10 + 5

• 15 cm

Second Side :

• 2x + 4

• 2 ( 10 ) + 4

• 20 + 4

• 24 cm

Third Side :

• 2x - 3

• 2 ( 10 ) - 3

• 20 - 3

• 17

So , all the sides are 15 cm , 24 cm and 17 cm .

Now , adding all these to find perimeter .

`\hookrightarrow \qquad \: 15 + 24 + 17`

`\hookrightarrow \qquad \: 39 + 17`

`\hookrightarrow \qquad \: \red{\underline{\boxed{\frak{56 \: cm}}}}`

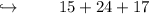
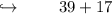
• Therefore , perimeter of triangle when value of x is 10 cm is 56 cm .

Alternative Solution : -

As above we have find the perimeter of triangle in term of x that is ( 5x + 6 ) cm. So we can put value of x as 10 in this to get perimeter. So ,

• 5x + 6

• 5 ( 10 ) + 6

• 50 + 6

• 56 cm

Therefore, perimeter of triangle is 56 cm .

#Keep Learning