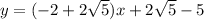Determine the equations of two lines that pass through the point (-1,-3) and are tangent to the graph of y=x² +1.

Question

asked Aug 9, 2023 28.0k views

1 Answer

Alfian Busyro · Answer 1 · 2023-08-13T23:23:05+0000

Answer:

Given equation:
y=x^2+1

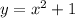
Therefore, we can say that any point on the curve has the coordinates
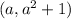(a, a^2+1) (where a is any constant)

To find the gradient of the tangent to the curve at any given point, differentiate the equation.

Given equation:

y=x^2+1

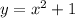
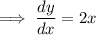
$\implies (dy)/(dx)=2x$

Therefore, the gradient at point
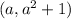(a, a^2+1) is

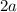
Using the point-slope form of linear equation, we can create a general equation of the tangent at point
(a, a^2+1) :

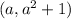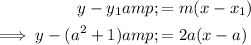
$\begin{aligned}y-y_1 & =m(x-x_1)\\ \implies y-(a^2+1)& =2a(x-a)\end{aligned}$

$\implies y=2ax-2a^2+a^2+1$

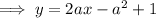
$\implies y=2ax-a^2+1$

Given that the tangents pass through point (-1, -3), input this into the general equation of the tangent:

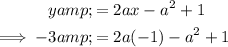
$\begin{aligned}y &=2ax-a^2+1\\ \implies -3 & =2a(-1)-a^2+1\end{aligned}$

$\implies 0=-2a-a^2+1+3$

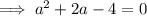
$\implies a^2+2a-4=0$

Use the quadratic formula to solve for a:

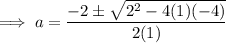
$\implies a=(-2\pm√(2^2-4(1)(-4)))/(2(1))$

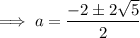
$\implies a=(-2\pm2√(5))/(2)$

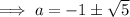
$\implies a=-1 \pm √(5)$

Input the found values of a into the general equation of the tangent to create the equations of the two lines:

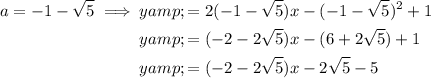
$\begin{aligned}a=-1+√(5)\implies y & =2(-1+√(5))x-(-1+√(5))^2+1\\ y & =(-2+2√(5))x-(6-2√(5))+1\\ y & =(-2+2√(5))x+2√(5)-5 \end{aligned}$

$\begin{aligned}a=-1-√(5)\implies y & =2(-1-√(5))x-(-1-√(5))^2+1\\ y & =(-2-2√(5))x-(6+2√(5))+1\\ y & =(-2-2√(5))x-2√(5)-5 \end{aligned}$

Therefore, the equations of the two lines that pass through the point (-1, -3) and are tangent to the graph of
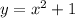y=x^2+1 are:

y=(-2+2√(5))x+2√(5)-5

y=(-2-2√(5))x-2√(5)-5