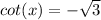Answer:
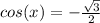
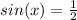
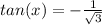
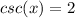
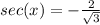
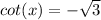
Explanation:
(I'll just use x for ease of writing)
We have the trig equation
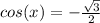 , and we know that its terminal side is in the 2nd quadrant. By using a unit circle, we can determine that the angle is
, and we know that its terminal side is in the 2nd quadrant. By using a unit circle, we can determine that the angle is
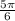 which has an ordered pair of
which has an ordered pair of
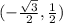
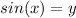 , so
, so
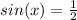
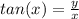 , so
, so

Now that we have sin, cos, and tan, we can just take the reciprocal of each of these to get our answers for csc, sec, and cot.
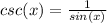 , so
, so
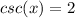
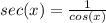 , so
, so
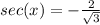
 , so
, so