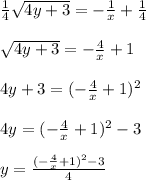Question

Given that y = 1.5 at x = -2. Find the function y = f(x) such that

dy/dx=√(4y+3)/x²

​

Answer 1

`y=((-(4)/(x)+1)^2-3 )/(4)`

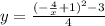
Explanation:

We are given the following information. y have the point
`(-2,(3)/(2) )` and
`(dy)/(dx) =(√(4y+3) )/(x^2)`

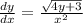
First, we need to separate the variables to their respective sides

`(1)/(√(4y+3) ) dy=(1)/(x^2) dx`

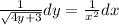
Now, we need to integrate each side

`\int (1)/(√(4y+3) ) dy=\int(1)/(x^2) dx`

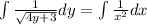
But first, let us rewrite these functions

`\int (4y+3)^{-(1)/(2) } dy=\int x^(-2) dx`

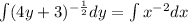
Before we can integrate, we need to have the hook for the first function. When we integrate
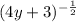`(4y+3)^{-(1)/(2) }`, we must have a lone 4 within the integral as well.

`(1)/(4) \int4 (4y+3)^{-(1)/(2) } dy=\int x^(-2) dx`

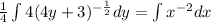
Now we can integrate each side to get

`(1)/(4) √(4y+3) =-(1)/(x) + c`

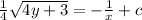
Now is the best time to use the given point in order to find the value of c.

`(1)/(4) \sqrt{4((3)/(2)) +3} =-(1)/(-2) + c\\\\(1)/(4)√(6+3) =(1)/(2) +c \\\\(3)/(4)=(1)/(2) +c\\ \\c=(1)/(4)`

Now we can plug in our value for c and then solve for y

`(1)/(4) √(4y+3) =-(1)/(x) + (1)/(4) \\\\√(4y+3)=-(4)/(x) +1\\ \\4y+3=(-(4)/(x) +1)^2\\\\4y=(-(4)/(x) +1)^2-3\\\\y=((-(4)/(x) +1)^2-3)/(4)`