Question

In a group of 42 students, 9 study both Art and Biology.

10 study Biology but not Art.
7 study neither subject.
Given that a randomly selected student studies Art, what is the probability the student studies Art and Biology?

Answer 1

The probability the student studies Art and Biology is 0.2143.

Explanation:

Denote the events as follows:

A = a students studies Art

B = a students studies Biology

The information provided is:

N = 42

n (A ∩ B) = 9

n (A' ∩ B) = 10

n (A' ∩ B') = 7

Then the number of students who study Art but not Biology is:

n (A ∩ B') = N - n (A ∩ B) - n (A' ∩ B) - n (A' ∩ B')

`=42-10-7-9\\\\=16`

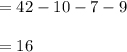
The number of students who study Art but not Biology is 16.

Compute the probability the student studies Art and Biology as follows:

`P(A\cap B)=(n (A\cap B))/(N)`

`=(9)/(42)\\\\=(3)/(14)\\\\=0.2143`

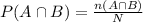
Thus, the probability the student studies Art and Biology is 0.2143.