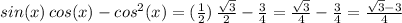Question

If cot x=v3, calculate (sin x)(cos x)-cos²x

Answer 1

`sin(x)\,cos(x)-cos^2(x)=(√(3) -3)/(4)`

Explanation:

Recall the Pythagorean identity for cotangent:

`1+cot^2(x)=csc^2(x)`

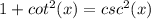
where the cosecant is the reciprocal of the sine function. So, since we know the value of the cotangent of the angle, we can derive the value of the square of the sine:

`1+cot^2(x)=csc^2(x)\\1+(√(3))^2=(1)/(sin^2(x)) \\1+3=(1)/(sin^2(x)) \\4=(1)/(sin^2(x))\\sin^2(x)=(1)/(4)\\ sin(x)=+/-(1)/(2)`

We can also use the Pythagorean identity for sin and cos, to find the value of
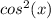`cos^2(x)` and of cos(x):

`cos^2(x)=1-sin^2(x)\\cos^2(x)=1-(1)/(4) \\cos^2(x)=(3)/(4)\\cos(x)=+/-(√(3))/(2)`

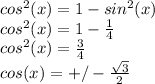
We also notice that since the cotangent is positive, the angle "x" must be located in either the firs or the third quadrant, where both sine and cosine have the same sign (both positive in the first quadrant, and both negative in the third quadrant.

Then the requested quantity can be written as:

`sin(x)\,cos(x)-cos^2(x)=((1)/(2)) \,(√(3) )/(2) -(3)/(4) =(√(3) )/(4) -(3)/(4)=(√(3)-3 )/(4)`