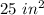Question

The length of a rectangle is x. The length and width add up to 10 inches. What is the maximum area of the rectangle? Please provide steps on how solve!

Answer 1

`Area=25\,\,in^2`

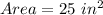
Explanation:

The length of the rectangle is unknown and is defined with the letter "x". Notice that the width of the rectangle is also unknown, so we can name it 'y".

Recall the formula for the area of a rectangle (length times width), and notice that it is this quantity the one we need to maximize (find the maximum possible value).

We use the other information provided to represent the rectangle's with (y) in terms of "x" :

length + width = 10 inches

x + y = 10

Therefore, y = 10 - x

Now we use this expression for "y" in the product for the area;

`Area= x\,*\,y\\Area=x\,(10-x)\\Area=10x-x^2\\Area=-x^2+10x`

Notice that this quadratic expression corresponds to a parabola with branches pointing down (negative leading term), so its maximum value would be given at the vertex of the parabola.

Now recall that the formula for the x-value of a parabola's vertex when its function is of the form
`f(x)=ax^2+bx+c`

is given by:

`x_(vertex)=-(b)/(2a)`

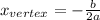
which in our case where "a" = -1 and "b" = +10, gives:

`x_(vertex)=-(b)/(2a)\\x_(vertex)=(-10)/(2(-1))\\x_(vertex)=(-10)/(-2)\\x_(vertex)=5`

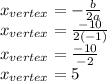
Then the maximum value for the Area can be obtained by replacing "x" with "5" in the area formula:

`Area=-x^2+10x\\Area=-(5)^2+10\,(5)\\Area=-25+50\\Area=25\,\,in^2`

Therefore, the area of the rectangle is
`25\,\,in^2`