Question

What is the third angle on a triangle with angels of 30 and 60?​

Answer 1

90 degrees

Explanation:

a triangles angles add up to 180

this means that you can add all the angles together and get 180

you can first add 30 and 60 and then subtract the sum from 180

30 + 60 = 90

180 - 90 = 90

the last angle is 90 degrees

Answer 2

Hey ! there

Answer:

• Third angle is equal to 90 degrees

Explanation:

In the question we are given with two angles of the triangles that are 30° and 60° . And we are asked to find the third angle of triangle .

For solving this question we must have knowledge of angle sum property which says that the sum of all the angles which are present inside the triangle ( interior angles ) is equal to 180°.

Solution : -

As we know that ,

• First angle = 30°

• Second angle = 60°

• Third angle = x (Here we are assuming third angle as x because in question it is not given and we have to find the value of third angle)

So ,

`\longmapsto \qquad \: 30° + 60° + x° = 180°`

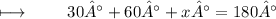
Step 1 : Adding 30° and 60° :

`\longmapsto \qquad \:90° + x° = 180°`

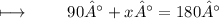
Step 2 : Subtracting 90° from both sides :

`\longmapsto \qquad \: \cancel{90°} - \cancel{90 ° } + x° = 180° - 90° \:`

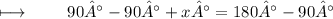
On further calculations , We get :

`\longmapsto \qquad \: \blue{\underline{\boxed{\frak{x° = 90°}}}}`

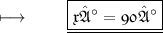
• Henceforth , value of x that is our third angle of triangle is 90° .

Verifying : -

Now we are verifying our answer by adding all the angles of triangle and equating them with 180° because of angle sum property. So ,

• Angle 1 + Angle 2 + Angle 3 = 180°

• 30° + 60° + 90° = 180°

• 90° + 90° = 180°

• 180° = 180°

• L.H.S = R.H.S

• Hence , Verified .

Therefore, our solution is correct .

#Keep Learning