Question

Find the point of diminishing returns (x comma y )for the function​ R(x), where​ R(x) represents revenue​ (in thousands of​ dollars) and x represents the amount spent on advertising​ (in thousands of​ dollars).

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

The point of diminishing returns (x , y ) is (11, 21462)

Explanation:

From the question we are told that

The function is
`R(x) = 10,000 -x^3 - 33x^2 + 800x , \ \ 0 \le x \le 20`

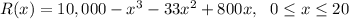
Here R(x) represents revenue (in thousands of​ dollars) and x represents the amount spent on advertising​ (in thousands of​ dollars).

Now differentiating R(x) we have

`R'(x) = -3x^2 +66x + 800`

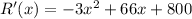
Finding the second derivative of R(x)

`R''(x) = -6x +66`

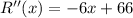
at inflection point
`R''(x) = 0`

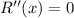
So
`-6x +66 = 0`

=>
`x= 11`

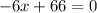
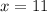
substituting value of x into R(x)

`R(x) = 10,000 -(11)^3 - 33(11)^2 + 800(11) ,`

`R(x) = 21462`

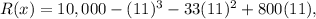
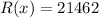
Now the point of diminishing returns (x , y ) i.e (x , R(x) ) is

(11, 21462)