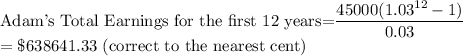Answer:
$638641.33
Explanation:
Adam earns $45,000 in his first year.
His salary increases by 3% each successive year. Therefore, his salary the next year is 103% of his previous year.
This is a geometric sequence where the:
- First Term, a= $45,000
- Common ratio, r =103%=1.03
(a)
Sum of geometric series
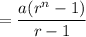
Substituting the given values, Adam's total earnings over n years
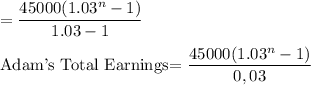
(b)When n=12 years