Answer:
The 95% confidence interval for the mean number of ounces of ketchup bottle is (23.8, 24.2).
Explanation:
The complete question is:
Suppose that a restaurant chain claims that its bottles of ketchup contain 24 ounces of ketchup on average, with a standard deviation of 0.8 ounces. If you took a sample of 49 bottles of ketchup, what would be the approximate 95% confidence interval for the mean number of ounces of ketchup per bottle in the sample?
Solution:
The (1 - α)% confidence interval for the population mean is:
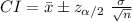
The information provided is:
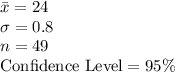
The critical value of z for 95% confidence level is:
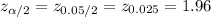
*Use a z-table.
Compute the 95% confidence interval for the mean number of ounces of ketchup per bottle as follows:
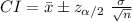

Thus, the 95% confidence interval for the mean number of ounces of ketchup bottle is (23.8, 24.2).