Answer:
D.) Converges; 256
Explanation:
x0= 192
x1 = 48 = 192/4
x2 = 12 = 192/(4 x 4)
Therefore, this series can be written as:
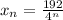
Applying limits at infinity:

Since the terms of the series tend to zero, we can affirm that the series converges.
The sum of an infinite converging series is:
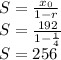
Thus, the answer is D.) Converges; 256