Question

A rich donor gives a hospital $ 960 comma 000 one year from today. Each year after​ that, the hospital will receive a payment 5 ​% larger than the previous​ payment, with the last payment occurring in ten​ years' time. What is the present value​ (PV) of this​ donation, given that the interest rate is 9 ​%?

Answer 1

$7,560,000

Step-by-step explanation:

To solve this problem, the Present Value (PV) of a growing annuity formula is used.

The Present Value of a growing annuity is the current value of a series of payments which grows or diminishes at a constant rate each period.

The formula below represents the PV of a growing annuity:

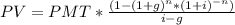`PV=PMT *((1-(1+g)^(n)*(1+i)^(-n)) )/(i-g)`, ............................................. (i)

where,

PV = Present Value = ?

PMT = Periodic Payment = $960,000

i = Interest Rate = 9% = 0.09

g = Growth Rate = 5% = 0.05

n = Number of periods = 10 years

Substituting these values in equation (i), we have

`PV=960000*((1-(1+0.05)^(10)*(1+0.09)^(-10) )/(0.09-0.05)`

`PV=960000*((1-(1.05^(10))*(1.09)^(-10)) )/(0.04)`

`PV=960000*((1-(1.63*0.42)))/(0.04)`

`PV=960000*((1-0.685))/(0.04)`

`PV=960000*(0.315)/(0.04)`

`PV=960000*7.875`

`PV=$7,560,000`

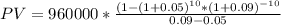
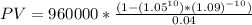
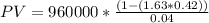
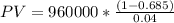
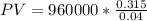
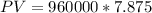
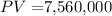
PV = $7,560,000