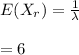Question

The lifespan of a car battery averages six years. Suppose the batterylifespan follows an exponential distribution.(a) Find the probability that a randomly selected car battery will lastmore than four years.(b) Find the variance and the 95th percentile of the battery lifespan.(c) Suppose a three-year-old battery is still going strong. (i) Find theprobability the battery will last an additional five years. (ii) Howmuch longer is this battery expected to last

Answer 1

Explanation:

Let X denote the life span of a car battery and it follows and exponential distribution with average of 6 years.

Thus , the parameter of the exponential distribution is calculated as,

μ = 6

`(1)/(\lambda) =6`

`\lambda = (1)/(6)`

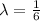
a) The required probability is

`P(X>4)=1-P(X\leq 4)\\\\=1-F(4)\\\\1-(1-e^(- \lambda x))\\\\=e^{-(4)/(6)`

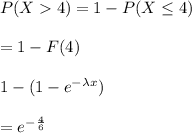
= 0.513

Hence, the probability that a randomly selected car battery will last more than four years is 0.513

b) The variance of the battery span is calculated as

`\sigma ^2=(1)/(((1)/(\lambda))^2 )\\\\\sigma ^2=(1)/(((1)/(6))^2 ) \\\\=6^2=36`

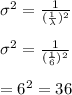
The 95% percentile
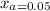`x_(a=0.05)` (α = 5%) of the battery span is calculated

`x_(0.05)=-(log(\alpha) )/(\lambda) \\\\=-(log(0.05))/(1/6) \\\\=-6log(0.05)\\\\=17.97 \ years`

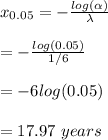
c)

Let
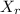`X_r` denote the remaining life time of a car battery

i)the probability the battery will last an additional five years is calculated below

`P(X_r>5)=e^(-5\lambda)\\\\=e^{-(5)/(6) }\\\\=0.4346`

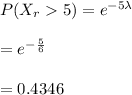
ii) The average time that the battery is expected to last is calculated

`E(X_r)=(1)/(\lambda) \\\\=6`