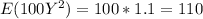Question

An individual who has automobile insurance from acertain company is randomly selected. Let Y be thenumber of moving violations for which the individualwas cited during the last 3 years. The pmf of Y is y p(y) 0 0.6 1 0.25 2 0.10 3 0.05 Suppose an individual with Y violations incurs a surcharge of $ 100 Y squared. Calculate the expected amount of the surcharge.

Answer 1

`E(100 Y^2) =100 E(Y^2)`

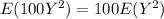
And we have that :

`E(Y^2) =\sum_(i=1)^n X^2_i P(X_i)`

And replacing we got:

`E(Y^2) =0^2 *0.6 + 1^2 *0.25 +2^2*0.10 +3^2 *0.05 = 1.1`

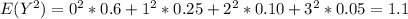
And finally we have:

`E(100 Y^2) =100 *1.1 = 110`

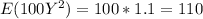
Explanation:

For this case we have the following probability masss function given:

Y 0 1 2 3

p(Y) 0.6 0.25 0.10 0.05

And we can define the surcharge with this expression
`100Y^2`

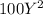
We want to find the expected value for the last expression and we can do it on this way:

`E(100 Y^2) =100 E(Y^2)`

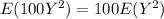
And we have that :

`E(Y^2) =\sum_(i=1)^n X^2_i P(X_i)`

And replacing we got:

`E(Y^2) =0^2 *0.6 + 1^2 *0.25 +2^2*0.10 +3^2 *0.05 = 1.1`

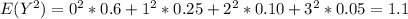
And finally we have:

`E(100 Y^2) =100 *1.1 = 110`