Answer:
Explanation:
Given that:
The investment amount in account = $ 320
The rate of interest is = 8.1% compounded quarterly
Compunded quarterly means 8.1% / 4 = 0.02025
The time period = t years
The objective is to write a function showing the value of the account after t years.
From compound interest , compounded monthly.
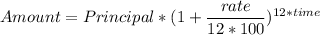
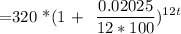
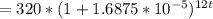
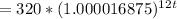
Thus; the function after t years
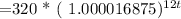
The percentage of growth per year is :
= (1 + 0.02025)^4 - 1
= 1.083493758 - 1
= 0.083493758
= 8.4 % (APY) yearly