Question

Of the mathematics degrees awarded in recent years, 76% were bachelor’s degrees, 21% were master’s degrees and the remaining 3% were doctorates. Moreover, women earned 52% of bachelors, 40% of masters and 22% of doctorates. What is the probability that a randomly chosen mathematics degree was a master's degree given that it was awarded to a woman? Give your answer to 4 decimal places.

Answer 1

0.1729 = 17.29% probability that a randomly chosen mathematics degree was a master's degree given that it was awarded to a woman

Explanation:

Bayes Theorem:

Two events, A and B.

`P(B|A) = (P(B)*P(A|B))/(P(A))`

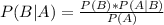
In which P(B|A) is the probability of B happening when A has happened and P(A|B) is the probability of A happening when B has happened.

In this question:

Event A: Given to a woman.

Event B: Masters degree.

21% were master’s degrees

This means that
`P(B) = 0.21`

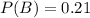
Women earned 40% of masters

This means that
`P(A|B) = 0.4`

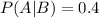
Probability of the degree being given to a women:

52% of 76%, 40% of 21% and 22% of 3%. So

`P(A) = 0.52*0.76 + 0.4*0.21 + 0.22*0.03 = 0.4858`

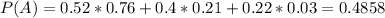
What is the probability that a randomly chosen mathematics degree was a master's degree given that it was awarded to a woman?

`P(B|A) = (0.21*0.4)/(0.4858) = 0.1729`

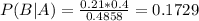
0.1729 = 17.29% probability that a randomly chosen mathematics degree was a master's degree given that it was awarded to a woman