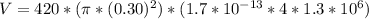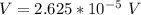Answer:
The average emf induce is
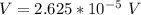
Step-by-step explanation:
From the question we are told that
The radius of the coil is

The number of turns is
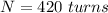
The frequency of the transition radio wave is
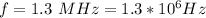
The magnetic field is
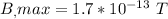
The time taken for the magnetic field to go from zero to maximum is

The period of the transmitted radio wave is
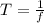
So
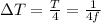
The potential difference can be mathematically represented as
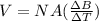
![V = NA ([B_(max) - B_(min) ] * 4f)](https://img.qammunity.org/2021/formulas/physics/college/70e70kgjiiw36ay06cvm7ebytyutd8p4ot.png)
Where
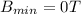
substituting values